Problem 1
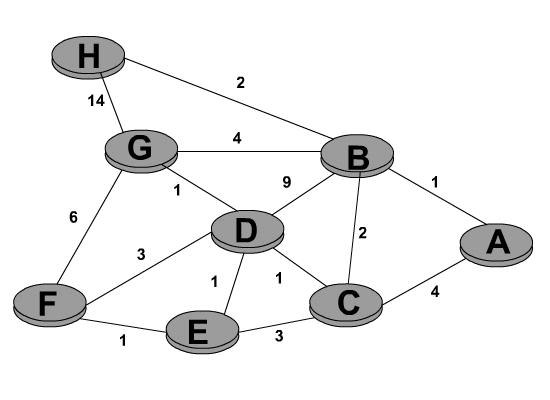
Consider the following network. With the indicated link costs, use Dijkstra's shortest path algorithm to compute the shortest path from F to all network nodes. Show how the algorithm works by computing a table similar to Table 4.3.
COMP 361 Tutorial -- Week 12
Problems from Chapter 4:
Problem 1Consider the following network. With the indicated link costs, use Dijkstra's shortest path algorithm to compute the shortest path from F to all network nodes. Show how the algorithm works by computing a table similar to Table 4.3.
|
Consider the network shown below and assume that the distance vector algorithm has converged to its stable state. Show (1) the distance table entries at node E, (2) the routing table entries at node E.

Consider the three-node topology shown as below, the link costs are c(X,Y) = 5, c(Y,Z) =6, c(Z,X) =2. Compute the distance tables after the initialization step and after each iteration of a synchronous version of the distance vector algorithm.

Consider a general topology and a synchronous version of distance vector algorithm (in one iterative step all the nodes compute their distance tables at the same time and then exchange them ). Suppose that at each iteration, a node exchanges its minimum costs with its neighbors and receives their minimum costs. Assuming that the algorithm begins with each node knowing only the costs to its immediate neighbors, what is the maximum number of iterations required until the distributed algorithm converges? Assume that the length of the longest minimum path between two nodes is d. Justify your answer.
Problem 5
Consider the network below with the given link costs.

Fill in the final values in Cís distance table that will result after running the distance vector routing algorithm with Poisoned Reverse.